Las transformaciones de Lorentz

Hoy vamos a deducir cuáles son las transformaciones de coordenadas que relacionan dos sistemas de referencia inerciales basándonos en los postulados de la relatividad especial. Antes de comenzar con el tema propiamente dicho vamos a definir lo que entendemos por unidades geométricas.

Unidades geométricas

El objetivo de emplear unidades geométricas es doble. De un lado, se trata de que en los diagramas espacio-tiempo las unidades que miden el espacio y el tiempo estén suficientemente compensadas como para que una magnitud tan grande como la velocidad de la luz — cuando se expresa en unidades convencionales — sea mucho más manejable.

De otro, buscamos que en la representación 4-dimensional podamos hacer geometría, hacer medidas de longitudes, áreas y volúmenes. Para ello es imprescindible que en todos los ejes coordenados tengamos las mismas unidades.

En realidad estamos muy acostumbrados a utilizar unidades geométricas. Lo hacemos desde hace ya mucho cuando en astronomía clásica se introdujo el concepto de año-luz: el espacio que recorre la luz en un año. De esta forma, medimos el espacio en años.

Si en lugar de traducir el espacio a unidades de tiempo nos planteamos pasar el tiempo a unidades de espacio obtenemos lo que sería un metro de tiempo: es el tiempo que emplea la luz en recorrer un metro. Así pues se tiene la siguiente fórmula

$t \quad \text{[en metros]} \quad = \quad c \times t \quad \text{[en segundos]}$

de modo que 1 metro de tiempo es un valor muy pequeño de segundos, en concreto: 1 metro de tiempo es $1/c$ segundos donde $c$ se expresa en metros/segundo con el conocido valor de $c=3\times10^8$ .

Con esta forma de proceder tenemos que:

1. los metros siguen midiéndose en metros,

2. los segundos ahora se miden en metros de acuerdo a la anterior expresión, y

3. la velocidad en unidades geométricas se relaciona con la velocidad clásica en los siguientes términos

$v \quad \text{[adimensional]} \quad = \quad \frac{v \quad \text{[en metros/segundo]}}{c}$

de suerte que la velocidad de la luz es unitaria (salvo el signo). A partir de ahora, y salvo que se indique lo contrario, trabajaremos siempre con unidades geométricas.

Propiedades de los sistemas inerciales

Partimos de dos sistemas $S$ y $S'$ que son inerciales con coordenadas $(x,y,z,t)$ y $(x',y',z',t')$ . Un sencillo ejercicio demuestra que el movimiento relativo entre ambos tiene velocidad $\vec{v}$ constante. A continuación vamos a definir dos propiedades que satisfacen los sistemas inerciales:

Definición

Un espacio se dice que es homogéneo si cada punto del espacio es indistinguible, i.e., si todos los puntos son equivalentes.

Definición

Un espacio se dice que es isótropo si cada dirección del mismo es indistinguible, i.e., si todas las direcciones son equivalentes. (Entendemos tanto dirección como sentido.)

Dado cualquier sistema de referencia inercial $S$ con coordenadas $(x,y,z,t)$ , ¿qué podemos decir de $S$ en relación a estas dos propiedades? Se tienen los siguientes hechos:

1. Homogeneidad temporal. Todos los instantes de tiempo $t$ son indistinguibles y equivalentes para la física.

2. Homogeneidad espacial. Todos los lugares del espacio son indistinguibles y equivalentes para la física pues el espacio $(x,y,z)$ es euclídeo. (Hay un razón más profunda para esto: tiene curvatura seccional constante.)

3. Isotropía espacial. Todas las direcciones espaciales son igual de buenas e indistinguibles para la física. (Aquí estamos afirmando que nuestro espacio se curva por igual en todas las direcciones. En el caso de un sistema inercial la curvatura es cero en todas las direcciones.)

4. NO isotropía temporal. En relación a la dimensión temporal los dos (únicos) sentidos posibles son el futuro y el pasado. Evidentemente, ambos son distinguibles desde el punto de vista físico. Hay muchos procesos físicos que nos indican hacia dónde apunta la flecha del tiempo. El más evidente de todos es el aumento de la entropía. (¿Conoces alguno más?)

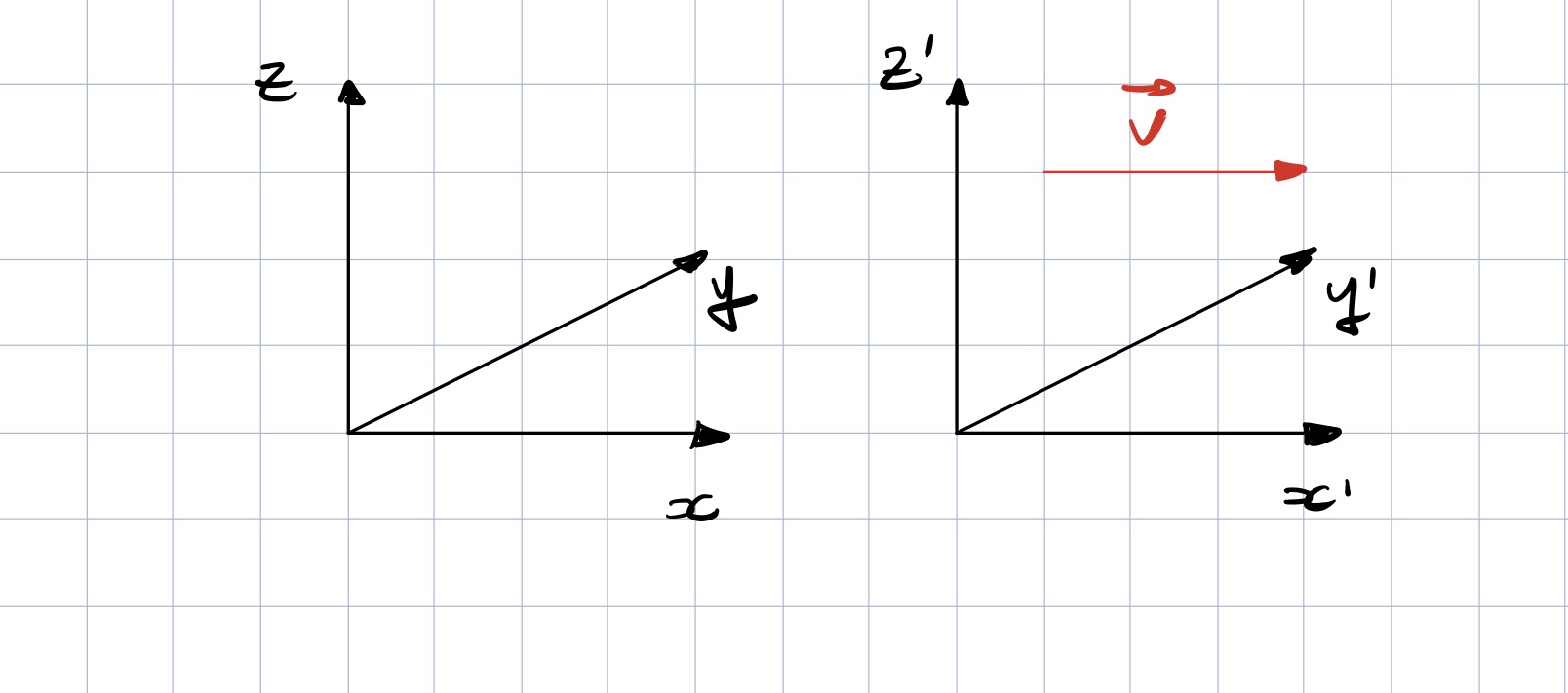
Utilizando la homogeneidad y la isotropía espacial es posible elegir coordenadas cartesianas en ambos sistemas $S$ y $S'$ para que los ejes $x$ y $x'$ sean coincidentes en todo instante de tiempo y apunten además en la dirección y el sentido de la velocidad relativa que relaciona a ambos sistemas. Utilizando ahora la homogeneidad temporal podemos elegir $t=t'=0$ exactamente cuando los orígenes de ambos sistemas sean coincidentes. Finalmente, utilizando de nuevo la isotropía espacial podemos rotar el plano $y'z'$ hasta hacer coincidentes los ejes $y'$ y $z'$ con los ejes $y$ y $z$ . (Coincidentes tanto en dirección como en sentido. Aquí es necesario asumir que las bases de cada uno de los sistemas tienen la misma orientación.)

Lo que resulta de hacer estas suposiciones está bien dibujado en el siguiente esquema:

Configuración estándar para dos sistemas inerciales

Esta configuración tan apañada se suele llamar configuración estándar y nos sirve para eliminar ruido y cuentas innecesarias. Ya en la época de Galileo se sabía que la mecánica para ambos sistemas se relaciona mediante las ecuaciones

$\begin{cases} x' = x -vt \\ y'=y \\ z'=z \\ t'=t \end{cases}$

Estas transformaciones de Galileo funcionan genial para la mecánica clásica de modo que las leyes de Newton son invariantes frente a este cambio de coordenadas. De estas transformaciones se deduce rápidamente la ley de adición clásica de velocidades. Así, si $(x(t),0,0,t)$ denota una partícula moviéndose por el eje $x$ en $S$ -coordenadas, sus coordenadas correspondientes en $S'$ vienen dadas por $(x(t)-vt,0,0,t)$ de suerte que la relación entre las velocidades está dada por

$\dot{x'}(t)=\dot{x}(t)-v.$

Las transformaciones de Lorentz

Observemos que los postulados de Einstein están en clara confrontación con estas transformaciones[mfn]Concretamente, el que está en conflicto es el segundo postulado.[/mfn]. Si $x(t)$ representa un rayo de luz entonces ambos sistemas deberían siempre medir la velocidad $c$ para $x$ por lo que obtendríamos $v=0$ . En consecuencia, debemos encontrar unas nuevas transformaciones para relacionar dos sistemas de referencia inerciales que sean compatibles con los postulados de Einstein.

A grandes rasgos necesitamos una transformación de la forma

$(x,y,z,t) \Longrightarrow (x',y',z',t')$

que sea compatible con los postulados y que relacione ambos sistemas. Evidentemente, existen infinitas posibilidades para elegir esta transformación así que vamos a acotar el campo de búsqueda imponiendo las restricciones físicas de la teoría. Por otra parte, debemos recordar que esto no es una deducción matemática sino que es una búsqueda cuya validez depende del resultado final no del proceso seguido. (La física es resultadista 😉 como Mourinho.)

En primer lugar supondremos que ambos sistemas se encuentran en configuración estándar. Esto se asumible ya que no hemos modificado nuestras hipótesis sobre las características de los sistemas de referencia inerciales.

Hecho 1. Las transformaciones son lineales

Las funciones de la transformación deben ser lineales. Esto se puede justificar usando diferentes argumentos. El primero y más directo sería diciendo que las únicas transformaciones que llevan rectas a rectas son las afines. (¿Esto es así?) ¿Qué hecho físico respalda esta restricción? Pues que se trata de sistemas de referencia inerciales por lo que las partículas libres se deben mover siguiendo líneas rectas en ambos sistemas.

No obstante, otra argumentación todavía más directa sería la que damos en el dibujo siguiente. Supongamos que una de las funciones no fuese afín. (Por ejemplo $x'$ no lineal en $x$ .) Al representar la gráfica de $x'(x)$ manteniendo el resto de coordenadas constantes observamos que la longitud de una varilla depende de su ubicación algo que entra en clara contradicción con la homogeneidad del espacio. El mismo argumento valdría para cualquier par de coordenadas en los sistemas $S'$ y $S$ .)

De esta forma reducimos así el problema de buscar 4 funciones al desafío de encontrar 20 números reales donde cuatro de ellos se corresponden con las constantes independientes de la transformación afín. Podemos asumir que estos cuatro números son cero ajustando el origen de nuestros sistemas, algo totalmente legítimo usando la homogeneidad del espacio y el tiempo.

Hecho 2. Las medidas perpendiculares al movimiento no se ven afectadas

Lo que queremos afirmar aquí es que las distorsiones y los cambios, en caso de haberlos, sólo se van a presentar en los ejes $x$ y $x'$ ya que tanto $y$ como $z$ se transforman en $y'$ y $z'$ sin cambios. Para demostrar esta afirmación vamos a hacer el siguiente experimento mental. Imaginemos que con el sistema $S'$ viaja un anillo perfectamente circular situado en el plano $x'=0$ y centrado en el origen de radio $r'$ . ¿Qué forma geométrica observa $S$ en relación a este objeto? El sistema $S$ debe apreciar también un anillo circular pues si no fuera así se violaría la isotropía espacial. Ahora bien, podría ocurrir perfectamente que el radio $r$ observado por $S$ fuera diferente que el radio $r'$ .

A continuación consideremos dos anillos circulares que en reposo son idénticos. Ponemos uno a viajar con $S$ y otro a viajar con $S'$ . En el momento en que $t=t'=0$ ambos sistemas coinciden en el origen por lo que ambos anillos están en el mismo plano $x=x'=0$ . ¿Qué ocurre con ambos anillos? ¿Chocan? ¿Pasa uno dentro del otro? ¿Otro dentro de uno?

Un examen cuidadoso de la cuestión obliga a que $r=r'$ ya que los dos sistemas son equivalentes para la física. Si, por ejemplo, el sistema $S$ observa que el radio del anillo de $S'$ se contrae entonces desde el punto de vista de $S'$ sería el anillo de $S$ el que sufre una contracción en su radio. Se llega así a una contradicción ya que los dos anillos no pueden pasar por dentro el uno con respecto al otro. La única salida posible es que ambos sigan manteniendo su radio invariante y que choquen al encontrarse en el origen.

Deducción de las transformaciones de Lorentz

A continuación presentamos en formato manuscrito la deducción de las transformaciones de Lorentz. Recordemos que se trata de una cuenta física y no matemática en el sentido de que las cosas valen cuando explican correctamente cómo funciona la realidad. Existe en la literatura una gran cantidad de modos y formas para calcular estas transformaciones pero a nosotros nos gusta especialmente la que mostramos a continuación. La referencia utilizada es:

World fastest derivation of the Lorentz transformations.
Alan Macdonald. Am.J.Phys. 49, 483 (1981)

En concreto, estamos utilizando una versión mejorada de este último artículo proporcionada por el propio Macdonald en su página web. Puedes consultar aquí el PDF de dicha mejora.

De esta forma, consideremos $S$ y $S'$ dos sistemas de referencia inerciales en configuración estándar. Por todo lo comentado en las anteriores secciones podemos reducir el estudio a dos dimensiones $(x,t).$ Para encontrar las transformaciones únicamente asumimos las siguientes hipótesis:

Hipótesis 1 (H1)

La velocidad de la luz es la misma en todos los sistemas de referencia inerciales, es decir, $c=1$ en unidades geométricas para todo observador.

Hipótesis 2 (H2)

El tiempo $t'$ de un reloj en movimiento respecto de un sistema $S$ a velocidad $v$ está afectado por un cambio de ritmo constante dado por una cierta función $\gamma(v)$ en relación al tiempo $t$ que registra el sistema $S$ .

Observemos que H2 hace referencia a un hecho que ya hemos estudiado en la dilatación del tiempo de modo que nosotros conocemos de modo explícito la función $\gamma(v)$ aunque nos podemos permitir el lujo de mantenerla oculta porque vamos sobradísimos. 😀

De hecho, obtendremos una expresión explícita para $\gamma(v)$ dentro del marco de esta deducción. Observemos también que $\gamma(v)$ sólo depende del módulo de la velocidad relativa entre los sistemas. (Más exactamente, del valor absoluto ya que estamos en 1D.)

En primer lugar se tiene que la línea del universo de $S'$ está dada por la ecuación $x'=0$ . Llamaremos $r$ a dicha recta. Observemos que esto ocurre, si y sólo si, $x=vt$ ya que el sistema $S'$ está en configuración estándar en relación a $S$ . Consideremos el siguiente experimento: el observador $S'$ emite un pulso de luz en $G$ , éste rebota en un espejo situado en la posición $E$ y regresa al observador $S'$ en $F$ . Podemos ilustrarlo con el siguiente diagrama:

El diagrama espacio-tiempo del experimento

La condición H2 puede expresarse en los siguientes términos: $t=\gamma t'.$ A lo largo de la recta $r$ se cumple que:

(1) $\begin{eqnarray*} t+x = \gamma t' + vt & = & \gamma t' + v\gamma t' = \\ & = & \gamma (1+v) t' = \gamma (1+v)(t'+x') \end{eqnarray*}$

donde en la ultima igualdad estamos usando que $x'=0$ al estar en la recta $r$ . Análogamente se tiene:

(2) $\begin{equation*} t-x = \gamma (1-v) t' = \gamma (1-v)(t' -x') \end{equation*}$

donde de nuevo usamos que $x'=0$ al estar en la recta $r$ . A continuación observemos que $t+x$ debe ser constante tanto en $F$ como en $E$ ya que la pendiente de la recta $L^{-}$ que une dichos puntos es -1. Lo mismo podemos afirmar para la cantidad $t'+x'$ .

Conclusión: la ecuación (1) es válida tanto en $F$ (obvio) como en $E$ .

Aplicamos el mismo argumento ahora para el rayo de luz que, partiendo de $G$ , alcanza el evento $E$ . Como ahora la pendiente de $L^{+}$ es 1, la ecuación (2) es válida tanto en $G$ como en $E$ .

Conclusión: las ecuaciones (1) y (2) son válidas en $E$ que es un lugar arbitrario del espacio-tiempo. Sumando ambas:

$\begin{eqnarray*} & t+x & = & \gamma (1+v)(t'+x')\\ +) \quad & t-x & = & \gamma (1-v)(t'-x') \\ = \quad & 2t & = & \gamma (2t'+2vx'). \end{eqnarray*}$

De suerte que nos queda

(3) $\begin{equation*} t = \gamma (t'+vx'). \end{equation*}$

Si en lugar de sumar hacemos la diferencia entre (1) y (2) llegamos a

(4) $\begin{equation*} x= \gamma (vt'+x'). \end{equation*}$

¿Cómo terminamos?

Final 1

La hipótesis $t=\gamma t'$ hace referencia a los tiempos $t$ que mide $S$ respecto de un reloj solidario con $S'$ que marca el tiempo $t'$ . Recordemos que esto es simplemente la fórmula que apareció en el reloj de luz para la dilatación del tiempo donde $t'=t_0$ en la fórmula

$t=\frac{t_0}{\sqrt{1-\frac{v^2}{c^2}}}.$

Así se llega a que

$\gamma(v)=\frac{1}{\sqrt{1-v^2}}$

que es lo que se conoce como el factor de Lorentz. (Recordemos que estamos trabajando en unidades geométricas.) Las transformaciones quedan, en definitiva, en los siguientes términos:

$\begin{cases} x=\frac{1}{\sqrt{1-v^2}}(x'+vt')\\ t=\frac{1}{\sqrt{1-v^2}}(vx'+t'). \end{cases}$

Final 2

Si escribimos $x=0$ en (4) entonces se tiene $x'=-vt'$ que describe el movimiento del origen de $S$ en términos del observador $S'$ . Así, $S$ tiene velocidad $-v$ respecto de $S'$ . Intercambiamos los roles de $S$ y $S'$ y la ecuación (1) quedaría así: