En esta lección vamos a estudiar la primera de las consecuencias que describe Einstein en su artículo de 1905. Nos referimos a que la simultaneidad es relativa: dos eventos que son simultáneos en un sistema de referencia inercial pueden no serlo en otro.
Vamos a explicar esta situación realizando el siguiente experimento. Imaginamos un vagón de tren de longitud 
(el resto de dimensiones son irrelevantes) que se desplaza a velocidad 
respecto de una estación de tren. (El signo positivo simplemente nos indica que el vagón se desplaza a la derecha.) Vamos a pensar que en cada uno de los extremos del vagón existe una lámpara o una bombilla. También, supongamos que exactamente en el centro del vagón tenemos un dispositivo fotosensible de dos caras de modo que, si recibe al mismo tiempo las dos señales luminosas, el dispositivo explota.
Bien, vamos a denotar por 
al suceso en el que la bombilla de la izquierda emite su pulso de luz y denotaremos por 
al suceso en el que la bombilla de la derecha emite su señal. El esquema sería algo así:
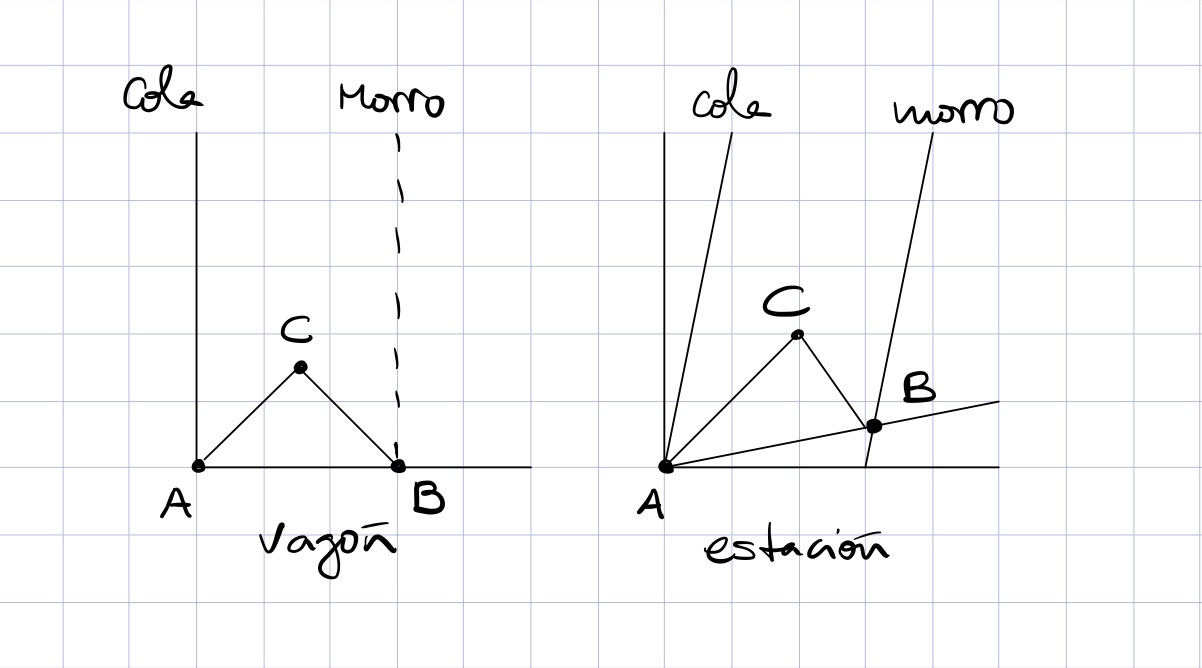
En el sistema de referencia del vagón podemos pensar que el origen está en el extremo izquierdo del mismo. Así, si otorgamos coordenadas a los sucesos y tendríamos algo así:
![\[ A = (0,t_A) \quad \textrm{y} \quad B = (L,t_B). \]](https://gravitacion.es/wp-content/ql-cache/quicklatex.com-15aa84033e51eab3038a486005449f31_l3.png "Rendered by QuickLaTeX.com")
Supongamos ahora que los sucesos son simultáneos para el observador del vagón. Esto significa que 
. Además, como la célula fotosensible está justamente en el centro del vagón y ambos pulsos viajan a la misma velocidad, es claro que el dispositivo recibe de modo simultáneo ambos pulsos y el vagón explota. (También el observador. Son los daños colaterales de hacer ciencia.)
Observemos que la explosión es un hecho físico, algo real e independiente del observador y/o de las coordenadas que se estén utilizando.
Ahora nos ponemos en la piel de un observador que está a pie de vía, en la estación. Dicho observador asigna diferentes coordenadas a los eventos y aunque únicamente nos interesa investigar qué ocurre con la parte temporal. Llamamos 
y 
a los tiempos registrados por el observador de la estación para los eventos y respectivamente. Ahora únicamente puede suceder que: 1) 
o 2) 
. Vamos a suponer que 2) es cierto y llegaremos a una contradicción por lo que la única posibilidad restante es 1).
Bien, ¿cuál es la contradicción? Pues es claro que, si ambos sucesos son simultáneos para el sistema de la estación, el rayo que parte de llega antes al centro del vagón que el pulso que sale de . El motivo es bien sencillo: ambos van a la misma velocidad, muy alta pero finita, por lo que el vagón se desplaza levemente hacia la derecha en este lapso breve de tiempo. Así. el rayo que parte de emplea menos tiempo pues recorre menos distancia para llegar al centro del vagón. Justamente lo contrario le ocurre al que sale de : el centro del vagón se va alejando de él y debe recorrer mayor distancia por lo que emplea más tiempo.
Conclusión: los rayos no llegan al mismo tiempo por lo que el dispositivo no explota. ¡Contradicción! Así pues, la única opción que nos queda es 1): ambos sucesos no son simultáneos para el sistema de la estación.
¿Qué está ocurriendo realmente? Ocurre lo siguiente: para que ambos pulsos lleguen de forma simultánea al centro del vagón y la célula explote el suceso es previo al suceso en el sistema de referencia de la estación. En otras palabras, se tiene que 
.
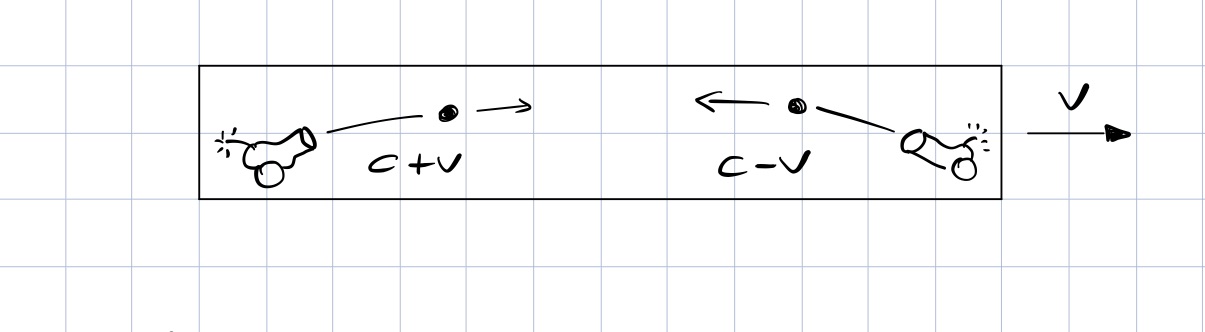
Desde un punto de vista clásico la situación sería la siguiente suponiendo que, en lugar de un rayo de luz, empleáramos balas de cañón:
Aplicaríamos entonces la ley de adicción de velocidades clásica y no habría fallo en la simultaneidad. Más adelante veremos que este experimento puede ilustrarse con una diagrama espacio-tiempo en los siguientes términos:
1 comentario
por favor pudieras mandarme mas ejemplos sobre la simultaneidad donde se deduzca la formula de la simultaneidad