GPS y Relatividad (II)

Estudiamos los efectos cuantitativos de la relatividad en el funcionamiento del GPS para discernir cuáles de ellos son los más importantes.

Biblio

Exploring Black Holes. An introduction to Einstein General Relativity
Edwin F. Taylor y John A. Wheeler. Addison Wesley. 2000.

Introduction to Relativistic Effects on the Global Positioning System
N.Ashby y J.J.Spilker. Progress in Astronautics and Aeronautics. 163 Capítulo 18.I.

Rasgos básicos del GPS

El sistema GPS incluye 24 satélites en órbita circular alrededor de la Tierra con período orbital de 12 horas. Los satélites se distribuyen en 6 planos orbitales y éstos están separados con el mismo ángulo. Cada satélite transporta un reloj atómico y emite señales de radio en las que codifica tanto su tiempo como su posición.

Analizando las señales de, al menos, cuatro de estos satélites, un receptor en la superficie terrestre con su microprocesador interno puede calcular su localización: latitud, longitud y altitud. Además, puede corregir su reloj para que esté continuamente sincronizado con los relojes atómicos de los satélites. (Véase la clase anterior.)

Los receptores de uso común tienen el tamaño de una calculadora, cuestan unos cientos de euros y una precisión horizontal del orden de 25 metros. Originalmente las señales del satélite contenían un ruido intencionado para hacer los receptores civiles poco precisos. Los receptores militares podían descodificar y eliminar dicho ruido. Desde la primavera del año 2000 esta peculiaridad fue eliminada. El sistema GPS ha revolucionado muchas áreas de la experiencia humana como la conducción, el vuelo, la exploración, la montaña, el rescate, la topografía y la geología.

Ejemplo

En una maniobra de aproximación de aterrizaje el aeropuerto utiliza un GPS en la torre de control y el avión lleva otro en la cabina. Los dos receptores están tan próximos que de esta forma se cancelan los errores de propagación de las señales a través de las capas altas de la atmósfera. De este modo, se tiene la posición del aeroplano con una precisión de menos de un metro.

La precisión en las medidas del tiempo que requiere el sistema GPS es tan alta que los efectos relativistas son vitales para su buen funcionamiento. Ya vimos en la clase anterior que los relojes funcionan de manera diferente según su posición en un campo gravitatorio. Además, tanto el satélite como el receptor en la Tierra tienen una velocidad relativa por lo que debemos tener presente el efecto de la relatividad especial y la dilatación del tiempo.

La importancia de sincronizar los relojes

En el operativo del GPS necesitamos que los relojes estén sincronizados. Para ello lo mejor es basarnos en el siguiente esquema:

Relojes estacionarios a diferentes alturas

En la lección Relojes en un campo gravitatorio elaboramos una estimación sobre la diferencia entre dos relojes que se encuentran situados a diferentes alturas dentro de un campo gravitatorio. La ecuación que obtuvimos fue

(1)   \begin{equation*} \nu_B=(1 + \frac{\Phi_A-\Phi_B}{c^2})\nu_A. \end{equation*}

donde \nu_A (resp. \nu_B) representaba la frecuencia que mide Alicia a mayor altura (resp. Bernardo a menor altura). Si identificamos la A de Alicia con el satélite, la B de Bernardo con el receptor GPS en la tierra y tomamos los inversos de las frecuencias, tendríamos ahora

(2)   \begin{equation*} t_s=(1 + \frac{\Phi_s-\Phi_r}{c^2})t_r \end{equation*}

donde ahora t_s (resp. t_r) denota el tiempo transcurrido entre dos tics sucesivos en el satélite (resp. entre la recepción de esos dos tics en la superficie terrestre). Vamos a estimar cuánto es exactamente esta diferencia de tiempo. Para ello, recordemos que

    \begin{eqnarray*} G & = & 6,67 \times 10^{-11} \text{ Nm}^2/\text{kg}^2,\\ M & = & 5,97 \times 10^{24} \text{ kg y} \\ r & = & 6,47 \times 10^6 \text{ m.} \end{eqnarray*}

Por otra parte, necesitamos saber la altura a la que se desplaza el satélite. La fuerza de la gravedad que actúa sobre el satélite se iguala con la fuerza centrífuga por lo que

    \[ \frac{GMm}{r_s^2}=m\frac{v^2}{r_s} \]

siendo m la masa del satélite y v su velocidad lineal. Despejamos ahora v y obtenemos

    \[ v=\sqrt{\frac{GM}{r_s}}. \]

Por otro lado, cuando el satélite completa una vuelta alrededor de la tierra se cumple

    \[ Tv=2\pi r_s. \]

Como T=12 horas tenemos el sistema

    \begin{eqnarray*} 12v & = & 2\pi r_s\\ v & = & \sqrt{\frac{GM}{r_s}} \end{eqnarray*}

del que se obtiene que

    \begin{eqnarray*} v & = & 4 \text{ km/s}\\ r_s & = & 2,7 \times 10^4 \text{ km.} \end{eqnarray*}

Hacemos algunas cuentas más. Para el potencial del satélite se tiene

    \[ \frac{\Phi_s}{c^2}=-\frac{GM}{r_sc^2}=-1,669689\times10^{-10} \]

mientras que para el potencial del receptor se llega a

    \[ \frac{\Phi_r}{c^2}=-\frac{GM}{rc^2}=-6,9534858\times10^{-10} \]

por lo que finalmente

(3)   \begin{equation*} t_s=(1 + 5,2837986\times10^{-10})t_r. \end{equation*}

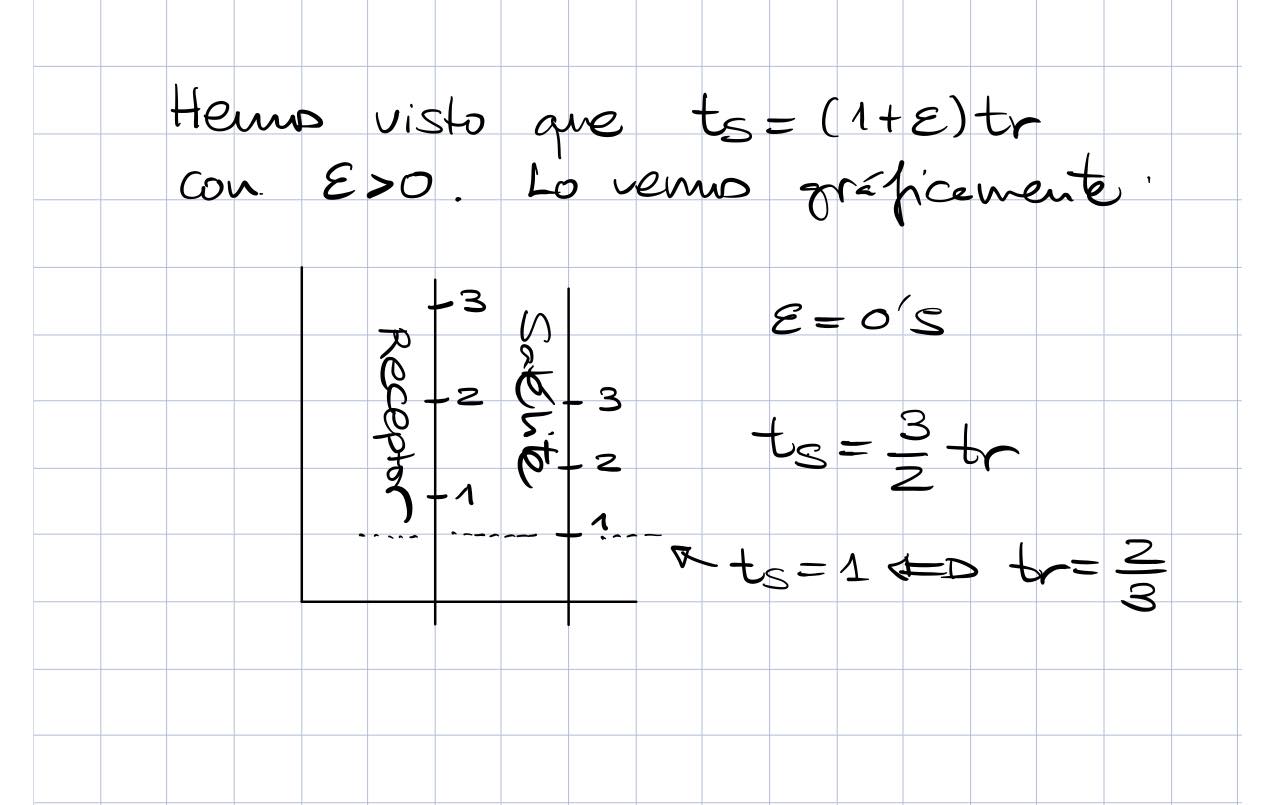
¿Qué significa esta última expresión? Pues que por cada segundo que pasa los dos relojes tienen una diferencia del orden de la mitad de un nanosegundo. A lo largo de un día transcurren unos 100.000 segundos por lo que se acumula un error de 50.000 nanosegundos grosso modo. Si cada nanosegundo supone un error de 0,3 metros, entonces estaremos cometiendo un error global en el día acumulado de 15 kilómetros. Completamente inadmisible.

A continuación veamos en un esquema cuál es la situación descrita en estas últimas cuentas.

Relojes en movimiento relativo a la misma altura

Tal y como explicamos en la clase anterior la relación entre el tiempo transcurrido en el satélite t_s y el tiempo observado por el receptor t_r está dada por

    \[ t_r=\frac{t_s}{\sqrt{1-v^2/c^2}}. \]

o equivalentemente

    \[ t_s=\sqrt{1-v^2/c^2}t_r. \]

Para estimar el valor de esta cantidad haremos una aproximación por Taylor en el valor de v^2/c^2 de suerte que

    \[ \sqrt{1-v^2/c^2}=1-\frac{v^2}{2c^2} \]

donde no tenemos en cuenta los términos de orden mayor o igual que dos en la variable v^2/c^2. (Obsérvese que v^4/c^4 es del orden 10^{2-33}=10^{-31}.) Si ahora introducimos los valores de v y c en la anterior expresión llegamos a

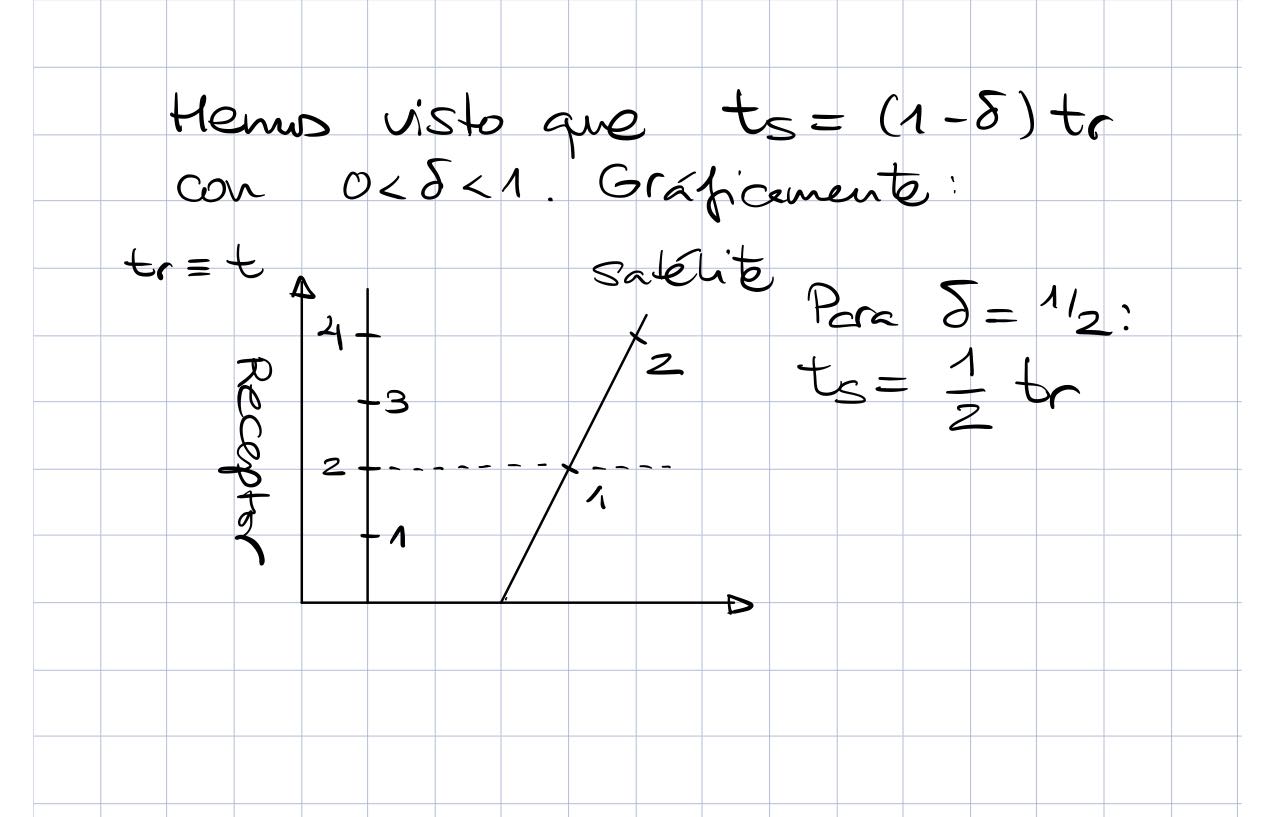
(4)   \begin{equation*} t_s=(1-0,83485\times 10^{-10})t_r. \end{equation*}

De nuevo, ¿qué significa esta última expresión? Pues que por cada segundo que transcurre en el satélite, el observador terrestre mide algo más de un segundo. Comparando la ecuación (3) con (4) se deduce que el efecto gravitatorio es del orden 5 veces mayor que el efecto dado por la diferencia de velocidades y de signo contrario.

Veamos ahora un esquema de cuál es la situación en un diagrama espacio-tiempo.

Otros efectos a tener en cuenta

El sistema GPS es muy complejo y existen otros muchos factores a tener en cuenta. En la bibliografía aportada puede consultarse la gran cantidad de aspectos técnicos que hay involucrados. En nuestro análisis, a muy bajo coste, podríamos hablar también de la velocidad de rotación terrestre que es del orden de 470 metros por segundo en el ecuador, unas 10 veces inferior a la velocidad del satélite.

No obstante, con los efectos ya explicados de la relatividad especial y general pensamos que ya hemos justificado suficientemente el por qué deben ser tenidos en cuenta a la hora de mantener operativo el sistema.

1 comentario

Deja una respuesta